16xAA font rendering using coverage masks, part I
Back when we started our Performance profiler, we knew we were going to do almost all the rendering of the UI ourselves. We soon had to decide how we were going to approach font rendering. We had a few requirements:
- We should be able to render any font on any size in real-time to ensure we can adapt to the system fonts & sizes our users have configured for Windows.
- Rendering fonts should be very fast, no stalls while fonts are being rendered.
- Our UI has a lot of smooth animation, text should be able to move smoothly across the screen.
- It should be legible on small font sizes.
Not being an expert on the matter at the time, I did a quick scan on the internet and found a variety of techniques to use for font rendering. I also had a chat with Michiel van der Leeuw, technical director at Guerrilla Games. They have experimented with multiple font rendering techniques and their rendering engine is certainly one of the best in the world. Michiel pitched an idea that he had in his mind for a new font rendering technique. While using an existing font rendering technique may have sufficed for us, I was intrigued by his idea and started implementing it, oblivious about the wondrous world of font rendering I was stepping into.
This blog series will explain the technique we’re using for font rendering in detail and is split into three parts:
- In part one, we will see how we render glyphs in real-time using 16xAA, sampled at a regular grid.
- In part two, we will move to a rotated grid to anti-aliase those horizontal and vertical edges nicely. We will also see how the final shader collapses almost entirely into a single texture and table lookup.
- In part three, we will see how we can rasterize the glyphs in real-time on Compute and CPU.
You can check out our profiler to see the results in action, but here’s a screen of the font “Segoe UI” rendered using our font renderer:
Here is a blowup of the letter ‘S’, rasterized at only 6×9 texels. The source vector data is rendered as an outline, the rotated sampling pattern is rendered using green and red rectangles. Because this is rendered on a resolution much higher than 6×9, the gray shades do not represent the final pixel shade – instead it displays the sub-pixel shade. This is a very helpful debugging visualization to see if all math on the sub-pixel level works out.
The idea: storing coverage instead of shade
The basic problem that font renderers need to address is how to map a font’s scalable vector data onto a fixed pixel grid. The way that the different techniques move from vector space to the final mapped pixels differs greatly. For most of these techniques, the curve data is first rasterized into temporary storage (like a texture) for some specific pixel size before being rendered. The temporary storage acts like a glyph cache: when the same glyph is rendered multiple times, the glyphs are retrieved from the cache and reused to avoid the need to rasterize them for each instance.
The difference between techniques is clearly visible in the way that the data is stored in the intermediate data format. For instance, the Windows font system rasterizes glyphs for a specific pixel size. The data that it stores is a shade per pixel. The shade represents a best effort approximation of the coverage of the glyph for that pixel. When rendered, the pixels are simply copied from the glyph cache to the target pixel grid. When transformed into the pixel format the data does not scale well and causes fuzzy glyphs when sized down and blocky glyphs when sized up. For that reason, glyphs are rendered for each target size into the glyph cache.
Signed Distanced Fields take a different approach. Instead of storing a shade, the distance to the nearest glyph edge for a pixel is stored. The advantage of this method is that this data scales a lot better for curved edges than shades do. When scaling a glyph up, curves remain smooth. The downside is that straight and hard edges get smoothed out. Advanced solutions like FreeType that store shade data achieve a much higher quality than SDF fonts can.
In cases where a shade for a pixel is stored, coverage needs to be calculated first. For example, stb_truetype gives some good insights about how coverage and shade can be calculated. Another common technique used to approximate coverage is to sample the glyph on a higher frequency than the target resolution and then count how many samples hit the glyph within a target pixel area. The hit count divided by the maximum number of possible samples will then determine the shade. Because the coverage is already translated to a shade for a specific pixel grid resolution and alignment, placing glyphs in between target pixels is not possible: the shade will not correctly reflect the actual coverage of the samples over the target pixel window. For this reason, and some other reasons that we will discuss later, such systems do not support sub-pixel movement.
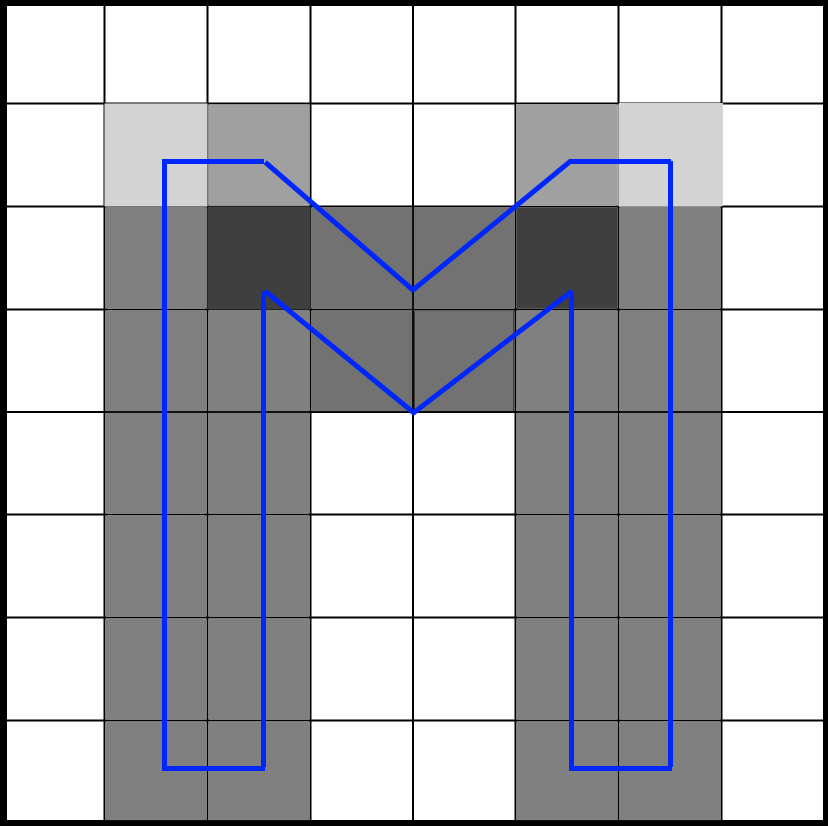
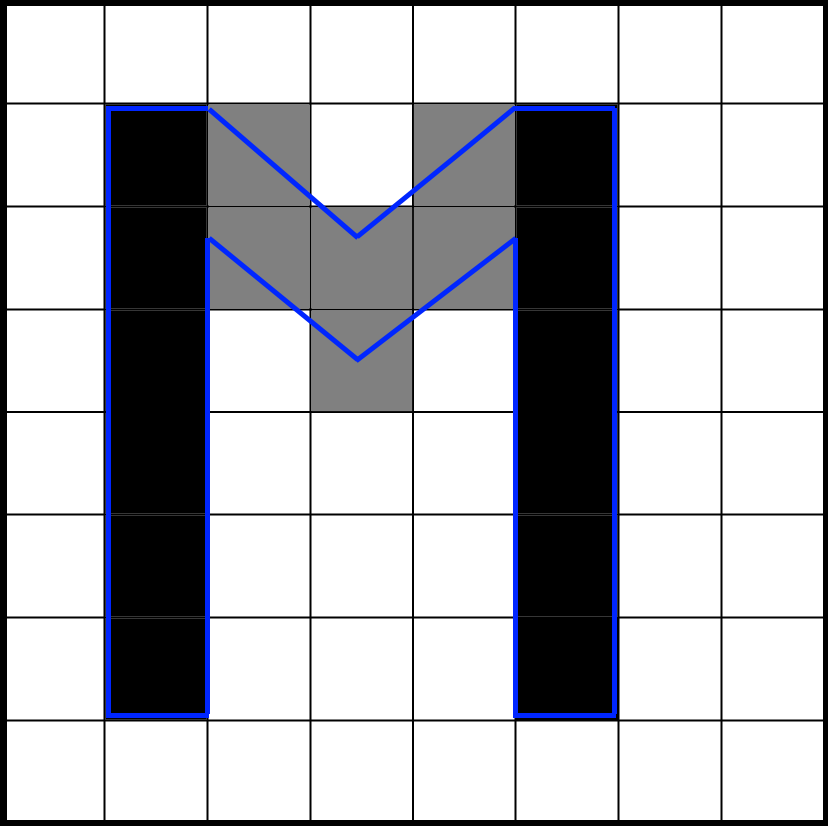
But what if we want to move the glyph freely between pixels? When the shade is already pre-calculated, we cannot know what the shade would be if it moved between pixels in the target pixel area. However, we can postpone the transformation from coverage to an actual shade until it is rendered. To do so, we don’t store shade, we store coverage. We sample a glyph on a frequency that is 16 times higher than the target resolution, and for each sample we store a single bit. When sampling on a 4×4 grid, we only have to store 16 bits per pixel. This is our coverage mask. During rendering, we will need to count how many bits fall within our target pixel window – a pixel window that has the same resolution as our texel storage, but does not physically align to it. In the following animation you can see a part of a glyph (blue-ish) that is rasterized onto four texels. Each texel is divided into a grid of 4×4 cells. The gray rectangle represents a pixel window that dynamically moves over the glyph. At runtime the number of samples that fall within the pixel window is counted to determine the shade.
A quick word on common font rendering techniques
Before discussing the implementation of our font rendering system, I first want to quickly explain a bit more about basic techniques used in font rendering: font hinting and subpixel rendering (on Windows known as ClearType). You can skip over this if you’re just interested in the AA technique.
As I was implementing the renderer I found out more and more about the long history of font rendering. The research all focuses on one aspect of font rendering and that is to make it readable on small sizes. Making a great font renderer for big fonts is pretty easy, but making something that remains readable on small sizes is incredibly hard. The research on font rendering dates back a long way and the depth to which it is executed is amazing. See, for instance, the Raster Tragedy. It makes sense that this was a key element for computer scientists, as screen resolution was pretty low in the early days of computing. It must have been one of the early problems that OS builders had to tackle: how do you make text readable on low resolution devices? To my own surprise, high quality font rendering systems are very pixel-oriented. For example, a glyph is built in such a way that it starts on a pixel boundary, its width is a multiple of a number of pixels, and the contents are adjusted to fit pixels. This is known as grid-fitting. Having a background in computer games and 3D graphics where the world is built up in units and then projected back to pixels, this came as a bit of a surprise to me. What I found out is that this is a very important choice in font rendering.
To show you the importance of grid fitting, let’s look at a possible scenario where a glyph is rasterized. Imagine that a glyph is rasterized on a pixel grid, but the shape of the glyph does not match the grid alignment nicely:
The anti-aliasing will make the pixels on the left and right of the glyph equally grey. If the glyph is moved a little so that the glyph falls better on the boundary of the pixels, only a single pixel would be colored, and it would be full black:
Now that the glyph aligns nicely with the pixels, the colors aren’t smudged as much. The difference in sharpness is very large. Western fonts have many glyphs that have horizontal and vertical lines and if they don’t line up with the pixel grid in a nice way, the grey tones will make the font look fuzzy. The best anti-aliasing technique in the world cannot solve that.
As a solution, font hinting was introduced. Authors of fonts need to give hints in their font about how they would like their glyphs to be aligned to pixels if they do not align properly. The font rendering system then distorts those curves to make them fit the pixel grid. This greatly enhances the sharpness of the font, but it comes at a cost:
- The fonts are slightly distorted. Fonts don’t look exactly as intended.
- All glyphs need to be aligned to a pixel grid: the start of the glyph and the width of the glyph. So, animating them in between pixels is a no-go.
Interestingly, Apple and Microsoft chose different paths here. Where Microsoft goes for absolute sharpness, Apple tends to go for a more font-correct approach. On the internet you can see people complaining about the fuzziness of the fonts on Apple machines, while others favor Apple’s look. So, it’s partly a matter of taste. Here’s a post from Joel on Software, and here’s a post from Peter Biľak discussing this issue, but if you search around the internet, there’s a lot more to find about the subject.
As the DPI in modern screens is rapidly increasing, the question arises whether font hinting will still be as necessary in the future as it is now. As it stands now, I think font hinting is still very valuable for crisp font rendering. The technique in this article may, however, become an interesting alternative in the future as glyphs can be freely placed on the canvas and are not distorted. And, as it basically is an anti-aliasing technique, it can be used for any purpose, not just font rendering.
Finally, a quick word about subpixel rendering. Back in the day, people realized they could triple the horizontal resolution of a screen by utilizing the separate red, green and blue beams within a computer monitor. Each pixel is built from those beams and they are physically spread apart. Your eyes blends these values together to form a single color for a pixel. When a glyph covers only part of a pixel, only the beams that physically have overlap with the glyph are enabled, tripling the horizontal resolution. If you zoom in on your screen when you have a technique like ClearType enabled, you will see colors around the edges of your glyph:
Interestingly, the approach I will be discussing here can be extended to use sub-pixel rendering as well. I’ve even implemented a prototype of it. The only downside is that due to the added filtering that a technique like ClearType uses, we need to take more texture samples. It’s perhaps something for a future episode.
Rendering a glyph with a regular grid
We are going to assume that we have sampled a glyph at 16 times the target resolution and that we stored this in a texture. How we do this will be explained in part three of this series. The sampling pattern is a regular grid – meaning the 16 sampling points are evenly distributed over a texel. Each glyph is rendered to the same resolution as the target resolution, and we store 16 bits per texel, each bit corresponding to a sample. The order in which we store our samples is important as we will see during the evaluation of the coverage mask. All in all, the sampling points and their positions for a single texel look like this:
Fetching the texels
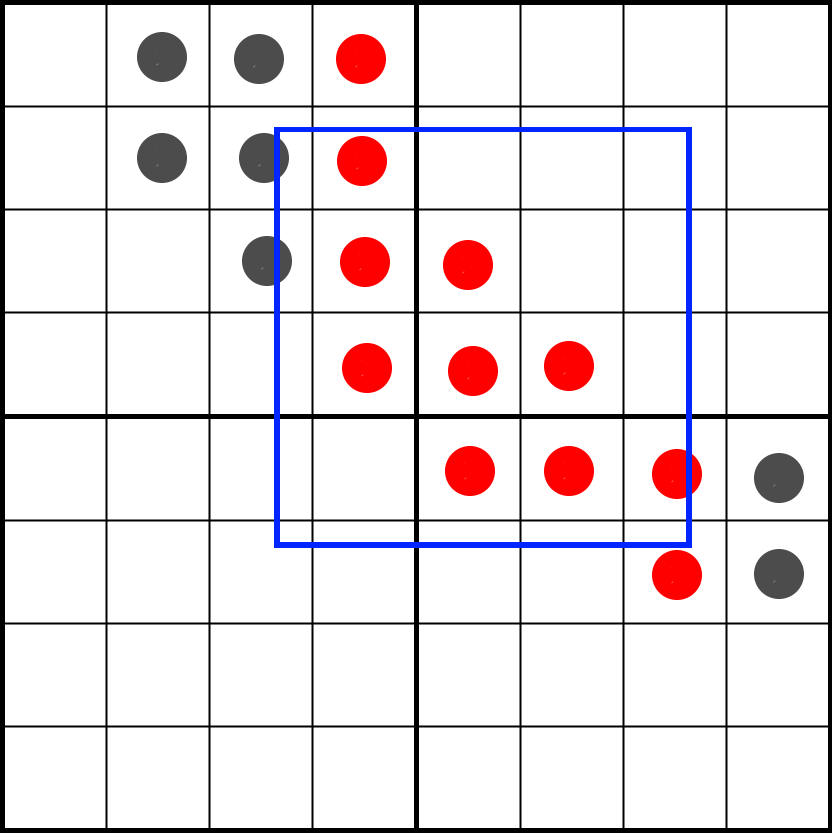
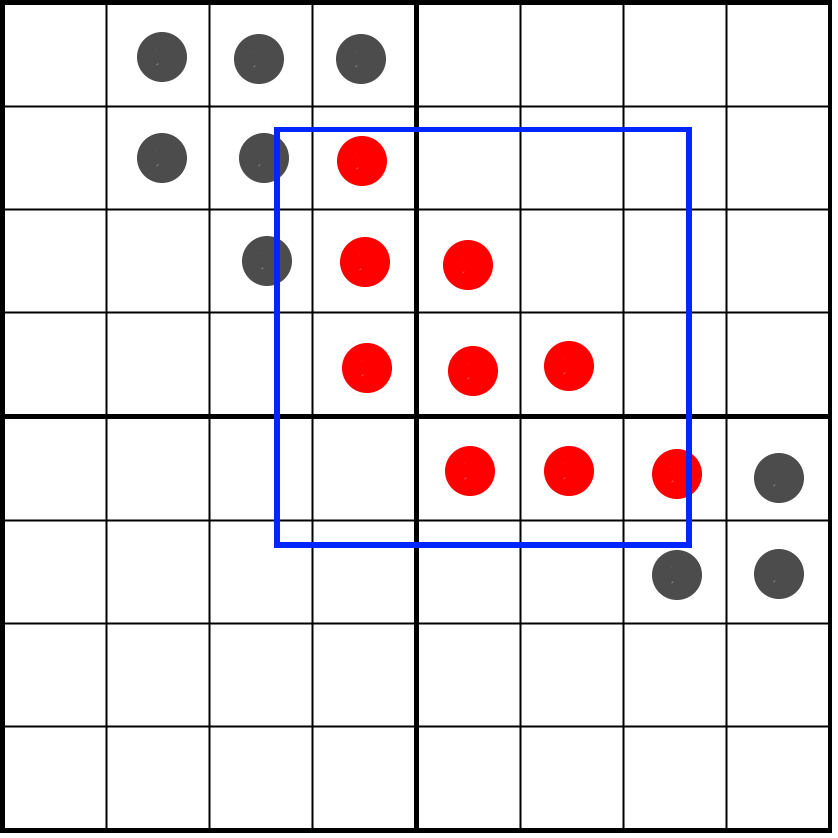
We are going to shift a pixel window over the coverage bits that we stored in the texels. The question that we need to answer, is: how many samples fall within our pixel window? The following picture illustrates this:
Here we see four texels with a partial glyph on them, one pixel (colored in blue) covering a portion of the texels. We need to determine how many samples our pixel window intersects. We first need to:
- Calculate the relative position of the pixel window compared to the 4 texels.
- Fetch the correct texels that our pixel window intersects.
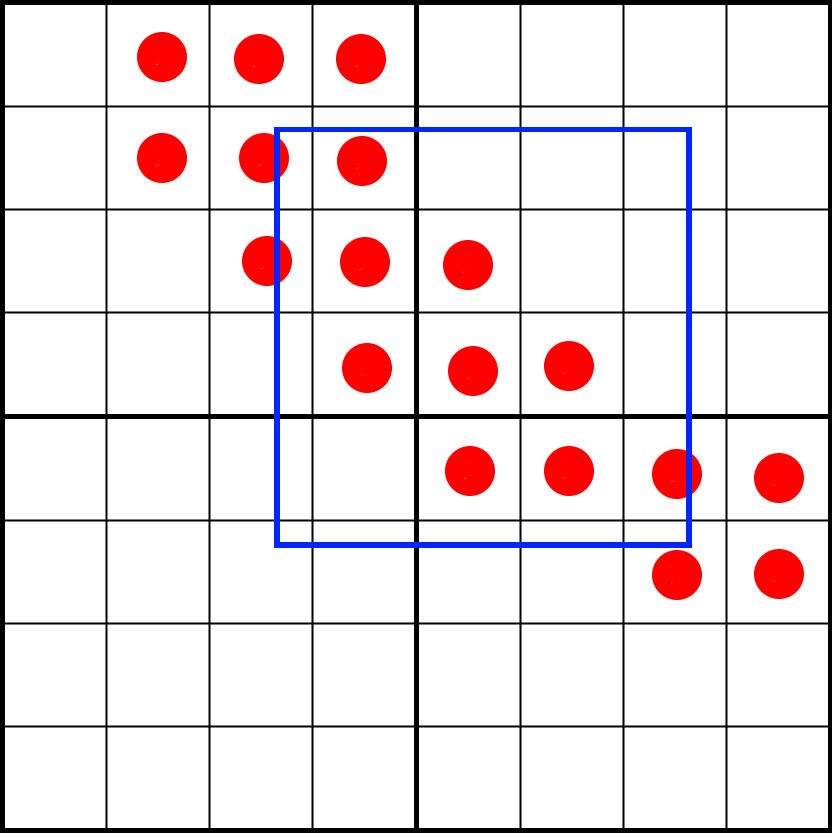
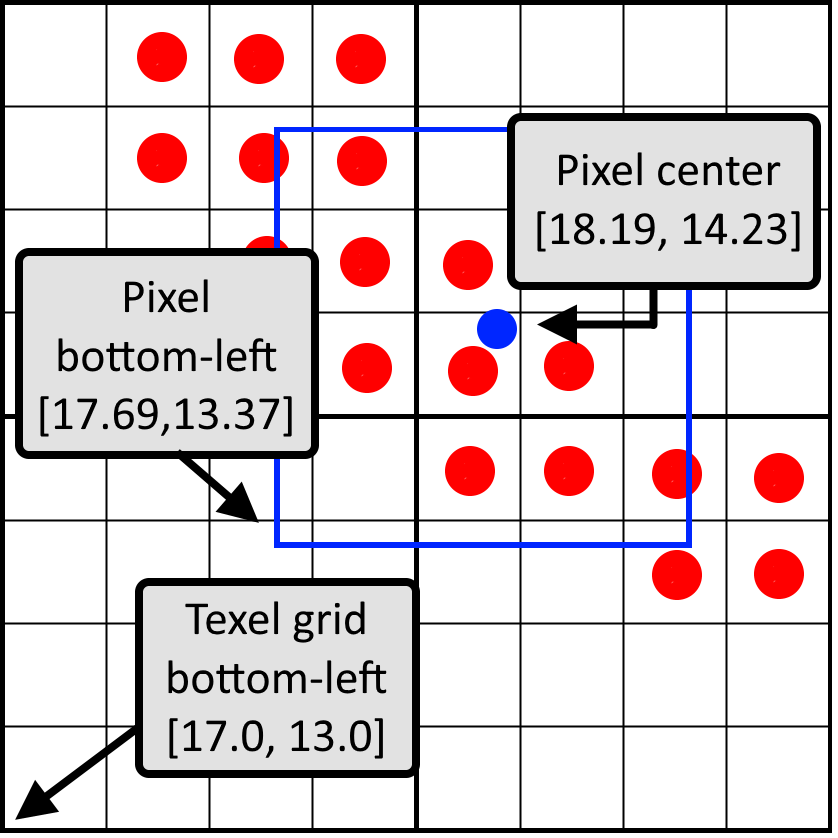
Our implementation is based on OpenGL, so the origin of our texture space is at the bottom left. Let’s start by calculating the relative pixel window position. The UV coordinate that was passed onto the pixel shader is the UV coordinate of the center of the pixel. Assuming the UVs are normalized, we can convert the UV to texel space first by multiplying with the texture size. Subtracting 0.5 from the pixel center brings us to the bottom-left corner of the pixel window. By flooring this value, we calculate the bottom-left position of the bottom-left texel. The following picture shows an example of those three points in texel space:
The difference between the bottom-left of the pixel and the bottom-left of the texel grid is the relative pixel window position in normalized coordinates. In this picture, the pixel window position would be [0.69, 0.37]. In code:
vec2 bottomLeftPixelPos = uv * size -0.5;
vec2 bottomLeftTexelPos = floor(bottomLeftPixelPos);
vec2 weigth = bottomLeftPixelPos - bottomLeftTexelPos;
We can fetch four texels at once with the textureGather instruction. This is only available on OpenGL 4.0 and above, so alternatively, you could perform four texelFetches. If we would just pass the UV to textureGather, a problem occurs when the pixel window aligns perfectly with a texel:
Here we see three horizontal texels with a pixel window (in blue) aligning exactly with the center texel. The weight as calculated is nearing 1.0, while textureGather picked the center and right texels instead. The reason is that the calculation performed by textureGather can be subtly different from the floating point calculation of the weight. Rounding differences between the calculation performed by the GPU and our floating point calculation of the weight results in glitches around pixel centers.
To solve this problem we need to make sure that our weight math is guaranteed to match textureGather’s sampling. To do so, we never sample at pixel centers, instead we always sample at the center of a 2×2 texel grid. From the calculated bottom-left texel pos that was already floored, we add a full texel to get to the center of the texel grid.
In this image, you can see that by using the texel grid center, the four sampling points used by textureGather will always be in the center of the texels. In code:
vec2 centerTexelPos = (bottomLeftTexelPos + vec2(1.0, 1.0)) / size;
uvec4 result = textureGather(fontSampler, centerTexelPos, 0);
The horizontal pixel window mask
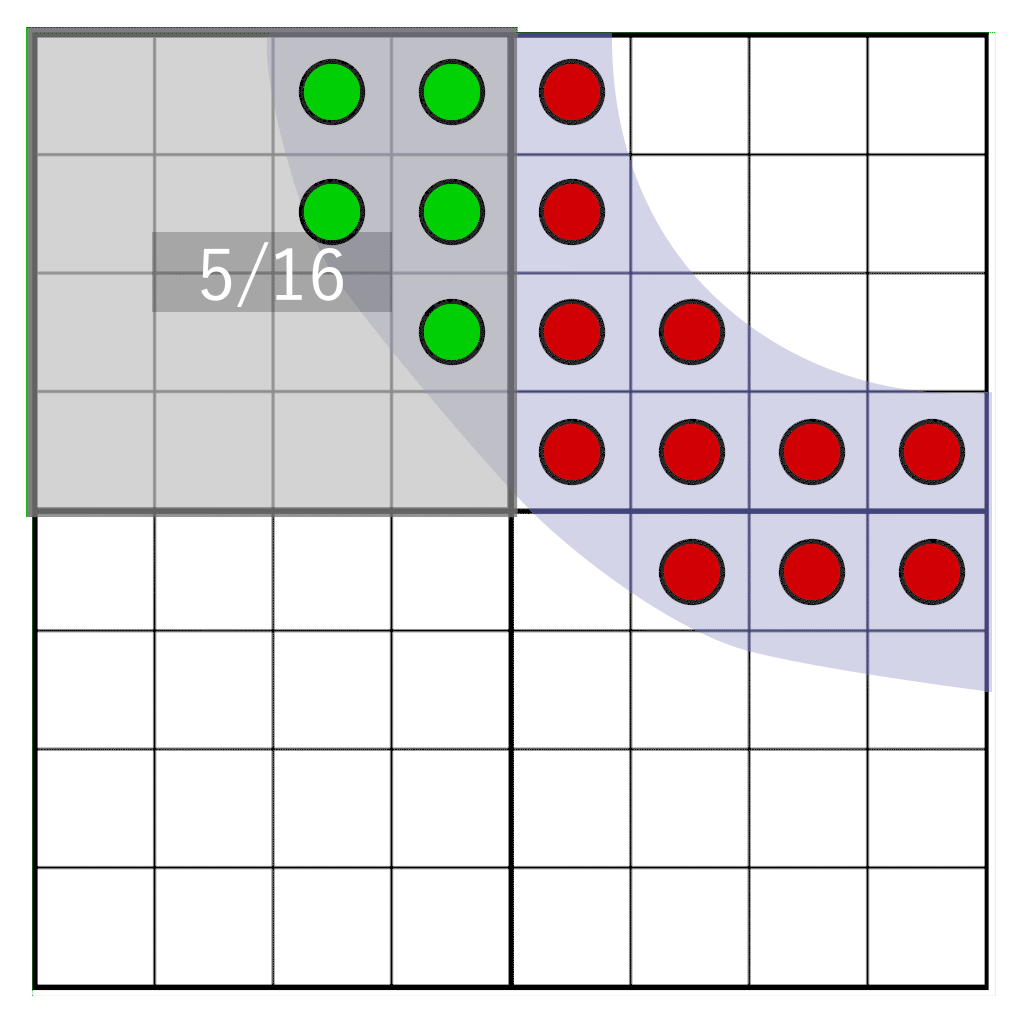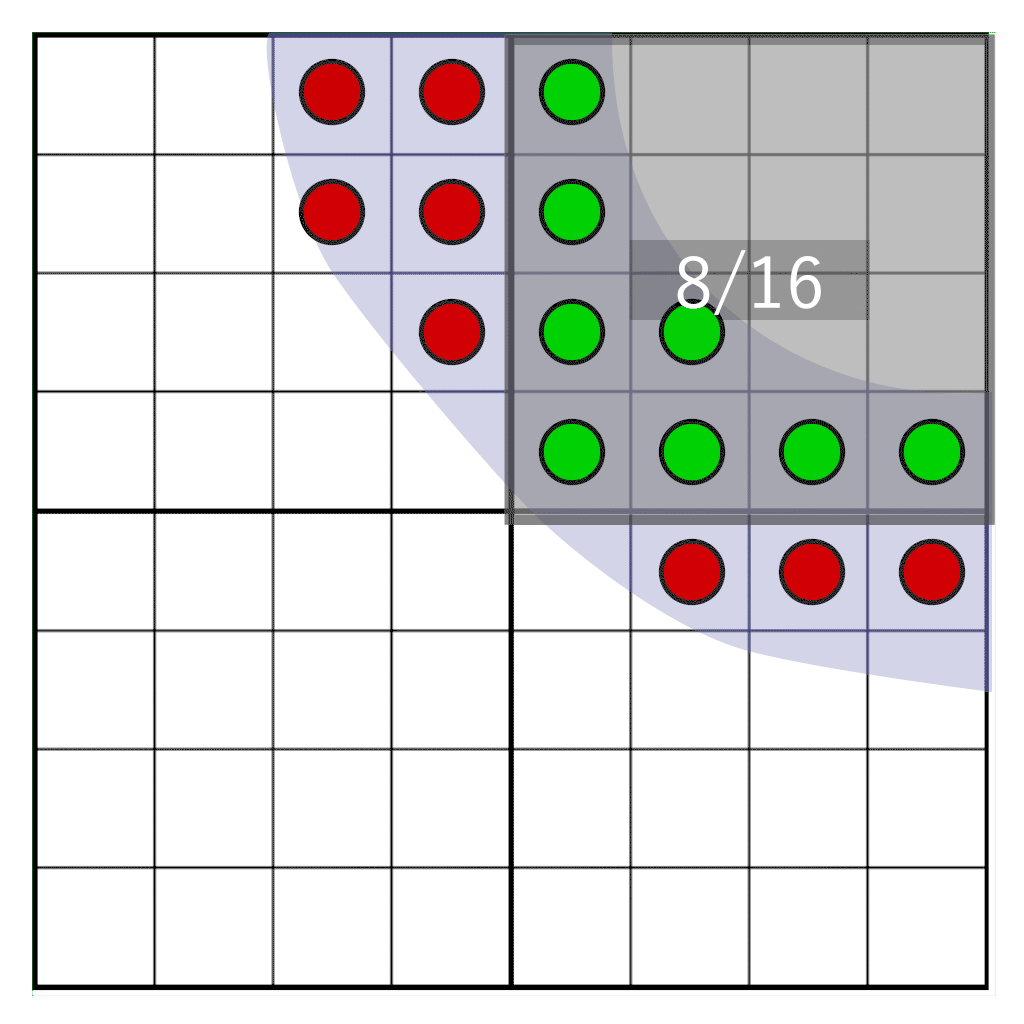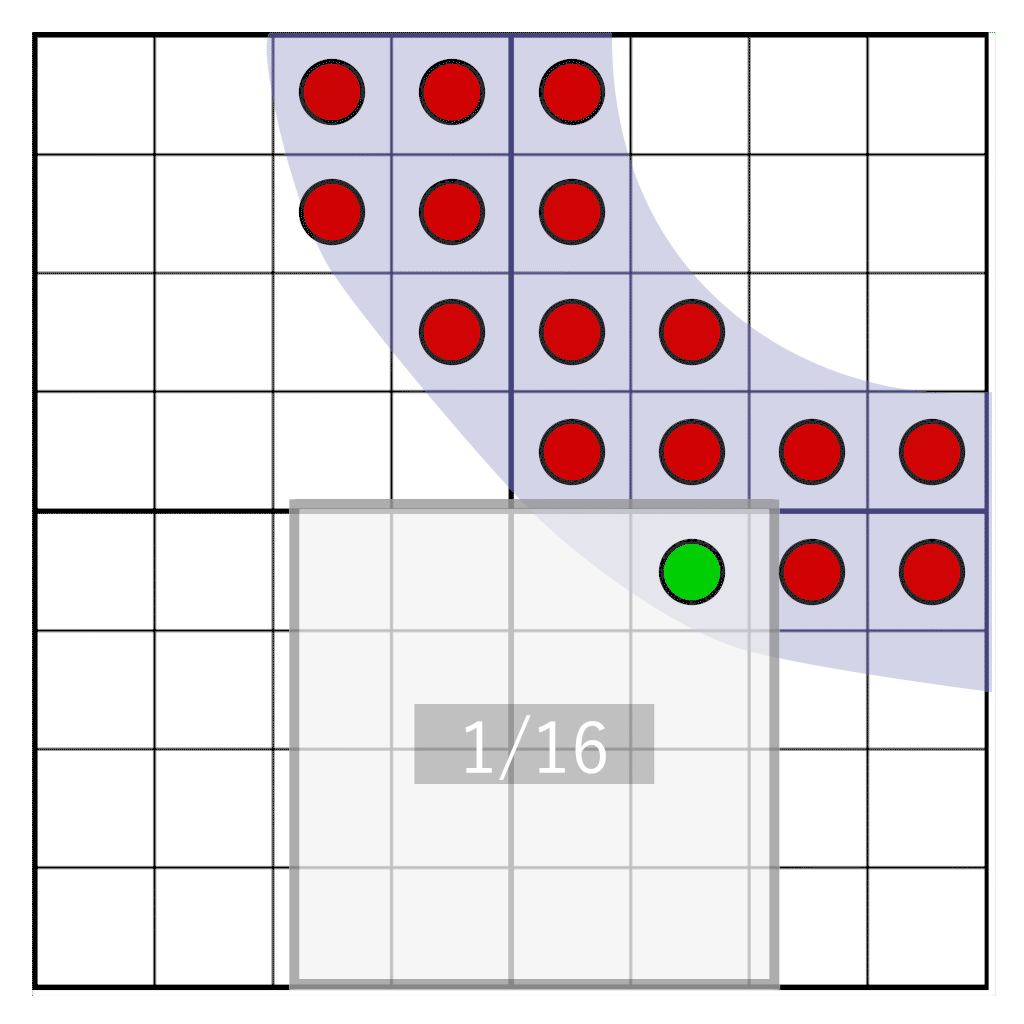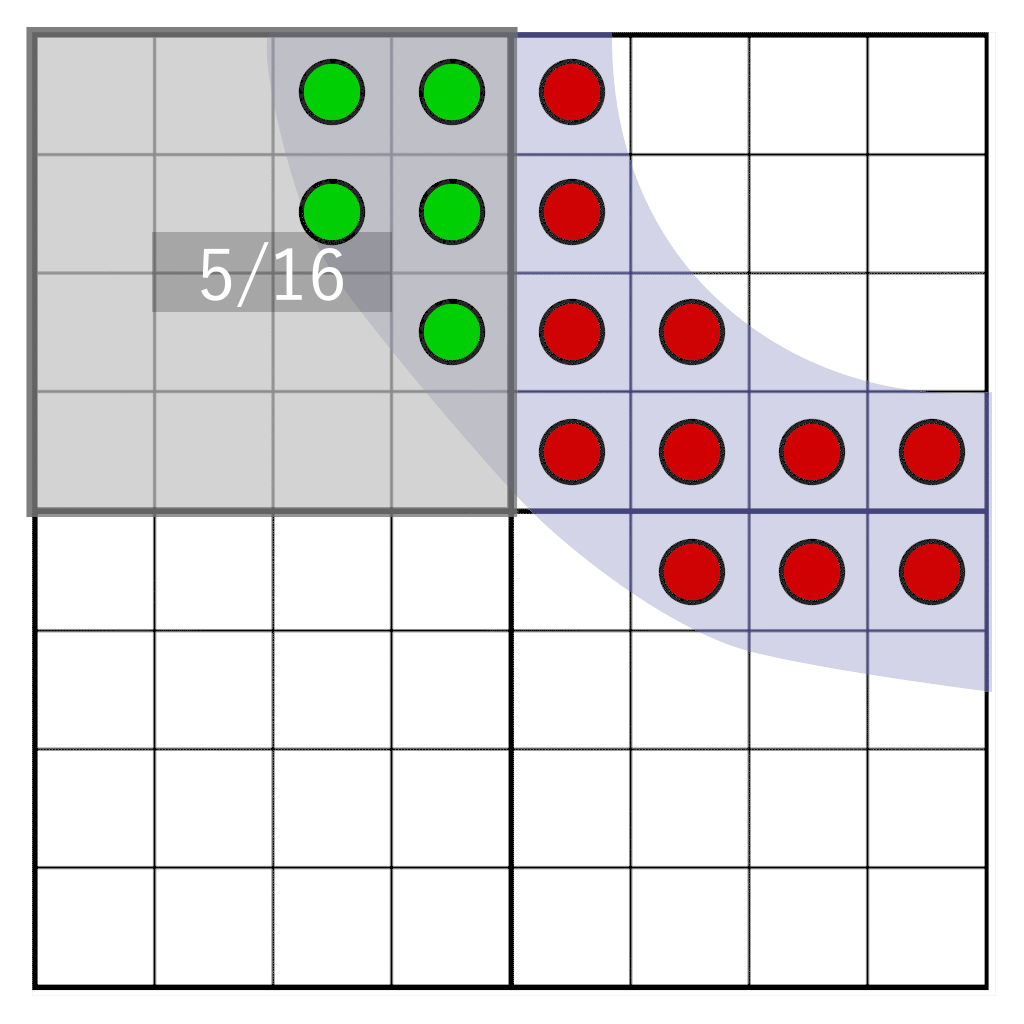
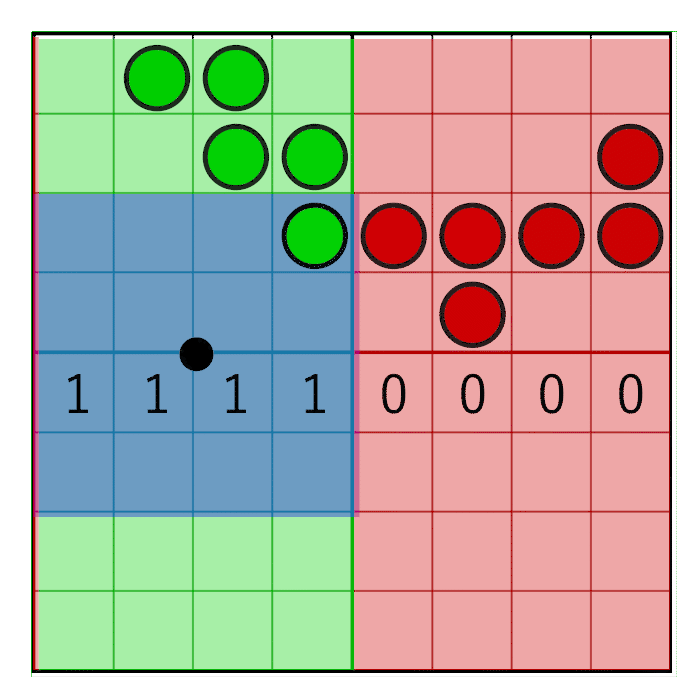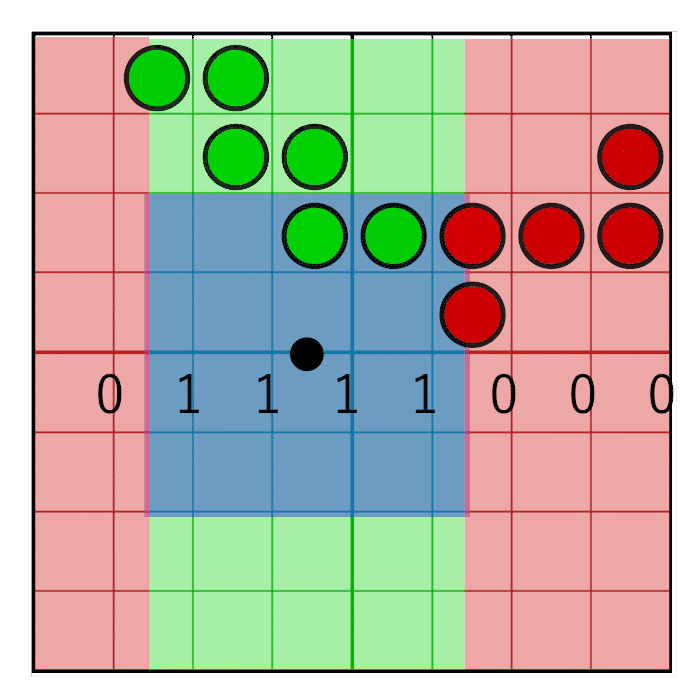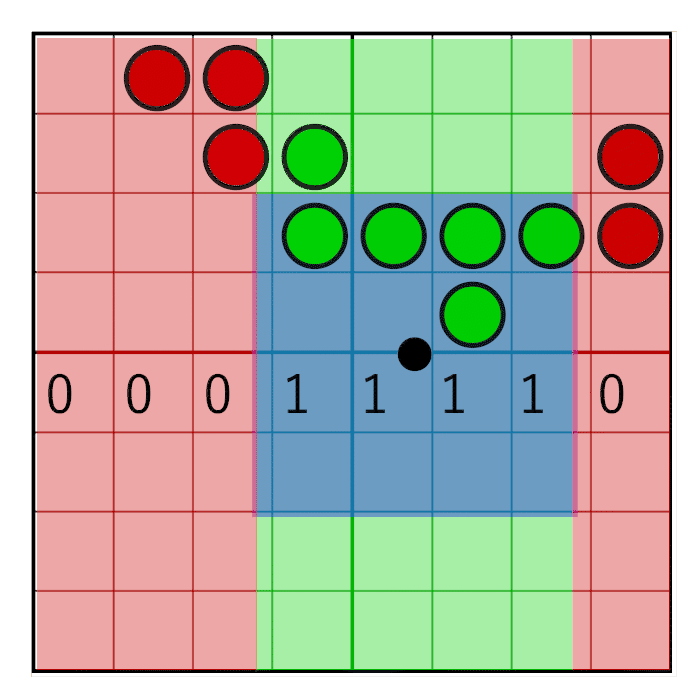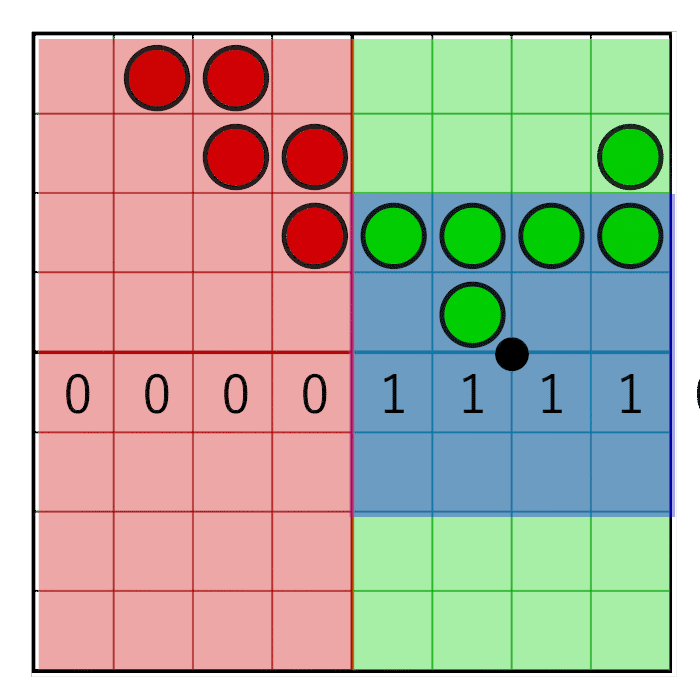
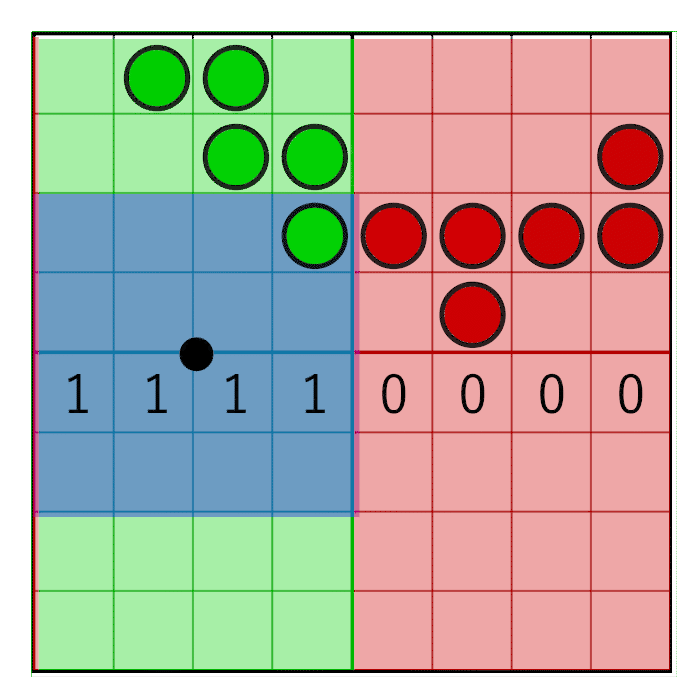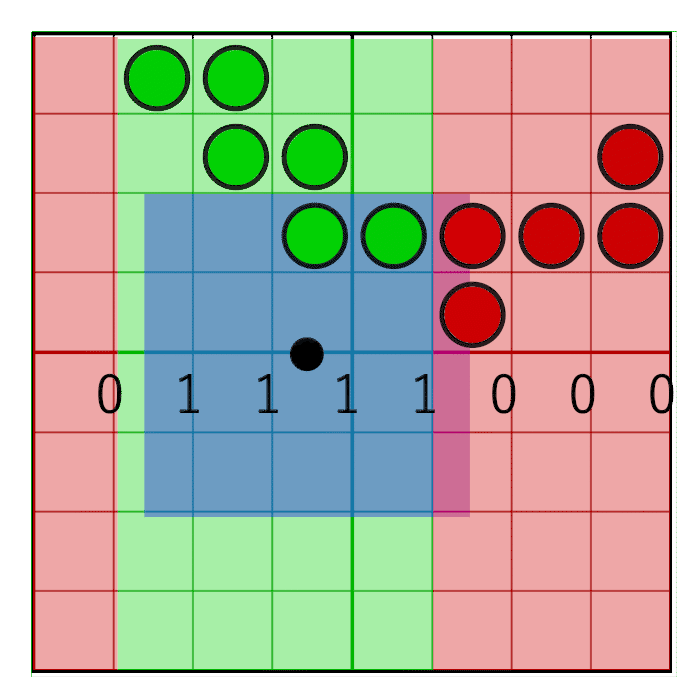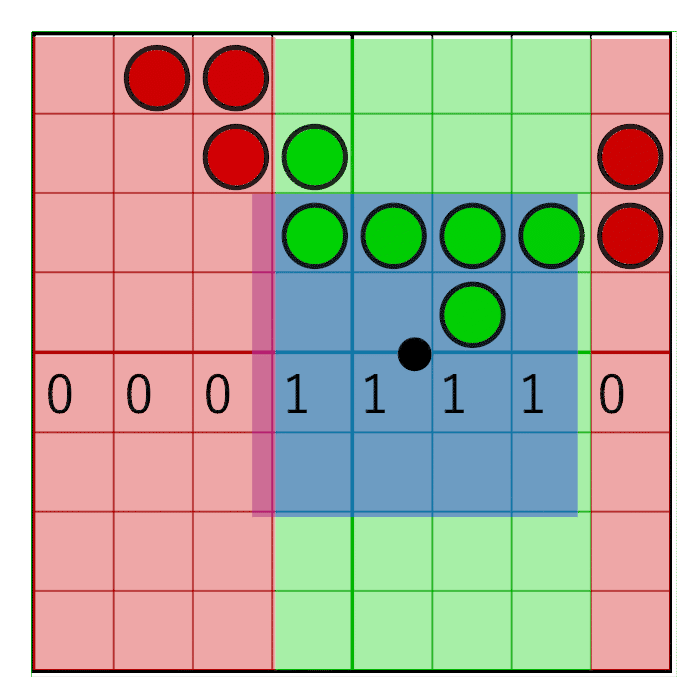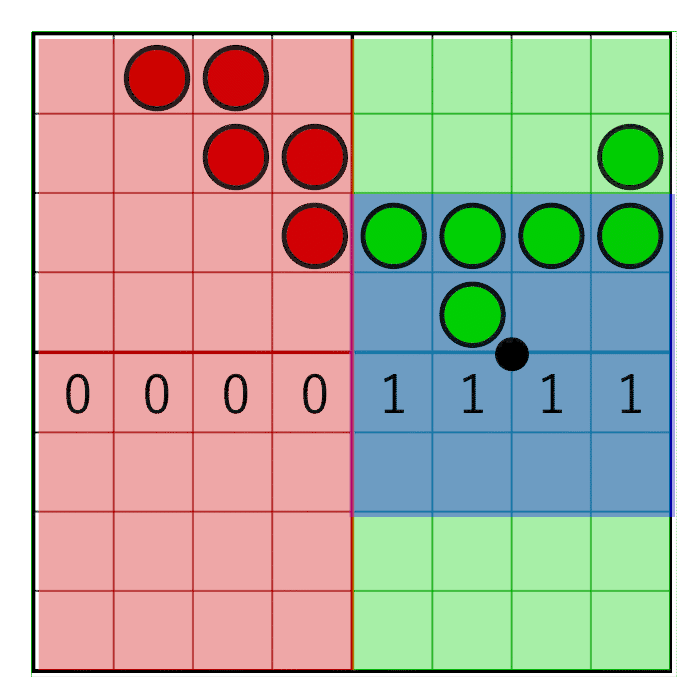
We have fetched four texels and together they form an 8×8 grid of coverage bits. To count the bits in the pixel window we first need to zero out the bits that are outside the pixel window. To accomplish this, we will create a pixel window mask and perform a bitwise AND between the pixel mask and the texel’s coverage masks. Horizontal masking and vertical masking is done separately.
The horizontal pixel mask should move along with the horizontal weight as shown in the following animation:
In the image you can see an 8 bit mask with the value 0x0F0 being shifted to the right (zero’s are inserted from the left). In the animation, the mask animates linearly with the weight, but in reality the bitshifting is a step-wise function. The mask changes value when the pixel window crosses a sample boundary. In the next animation this is visualized by the red and green columns animating in a step like fashion, switching value only when crossing the sample centers:
To make sure the mask doesn’t move on the cell’s edges but on the cell’s centre, a simple round will suffice:
unsigned int pixelMask = 0x0F0 >> int(round(weight.x * 4.0));
We now have a pixel mask for a full 8-bit row, spanning two texels. If we would choose the right kind of storage in our 16-bit coverage mask, there are ways to combine a left and a right texel, and perform the horizontal pixel masking for a full 8-bit row at once. However, this will become problematic in vertical masking when we move to rotated grids. Instead, we combine the two left texels with each other and the two right texels with each other to form two 32-bit coverage masks. We mask the left and right results separately.
The masks for the left texels use the upper 4 bits of the pixel mask and the masks for the right texels use the lower 4 bits of the pixel mask. For a regular grid, each row has the same horizontal mask, so we can just copy the mask for each row, and our horizontal mask is completed:
unsigned int leftRowMask = pixelMask >> 4;
unsigned int rightRowMask = pixelMask & 0xF;
unsigned int leftMask = (leftRowMask << 12) | (leftRowMask << 8) | (leftRowMask << 4) | leftRowMask;
unsigned int rightMask = (rightRowMask << 12) | (rightRowMask << 8) | (rightRowMask << 4) | rightRowMask;
To perform the masking, we combine the two left texels and the two right texels, and mask the horizontal rows:
unsigned int left = ((topLeft & leftMask) << 16) | (bottomLeft & leftMask);
unsigned int right = ((topRight & rightMask) << 16) | (bottomRight & rightMask);
The result could now look like this:
We can already count the bits from this result using the bitCount instruction. Instead of dividing by 16 we need to divide by 32 because there can still be 32 potential bits instead of the 16 bits that are left after vertical masking. Here is a full render of a glyph at this stage:
Here we see a blowup of the letter ‘S’ rendered using the source vector data (the white outline) and the sampling points visualized. When green, it is inside the glyph, when red, it is not. The gray shades show the shade as calculated so far. Font rendering has many points of failure, starting with rasterization, through the way data is stored in the texture atlas up until the calculation of the final shade. A visualization like this is invaluable in validating that all math works out exactly as planned. This is especially important for debugging sub-pixel level artifacts.
Vertical masking
Now we are ready for masking out the vertical bits. To mask out vertically, we use a slightly different method. To understand the vertical shift, it is important to remember how we’ve stored the bits: in row-major order. The bottom row occupies the four least significant bits and the top row occupies the four most significant bits. We can simply clear out the rows one by one by shifting them out based on the vertical pixel window position.
We will create a single mask that covers the entire height of two texels. In the end we want to keep four full rows of texels and mask the other ones out, so the mask is 4×4 bits which equals a value of 0xFFFF. Using the pixel window position, we shift out the bottom rows and clear the upper rows.
int shiftDown = int(round(weightY * 4.0)) * 4;
left = (left >> shiftDown) & 0xFFFF;
right = (right >> shiftDown) & 0xFFFF;
As a result, we’ve masked out the vertical bits outside the pixel window as well:
Now all we need to do is count the bits that are left in our texels, which is something we can do by using the bitCount operation, divide it by 16 and we have our shade!
float shade = (bitCount(left) + bitCount(right)) / 16.0;
The full render of our letter now looks like this:
For part two, we’ll crank it up a notch and see how we can apply this technique to rotated grids. We’ll be evaluating this bad boy:
And we’ll see how we can collapse almost everything into a few tables.
Thanks to Sebastian Aaltonen (@SebAaltonen) for his help with the textureGather issue and of course Michiel van der Leeuw (@MvdleeuwGG) for his ideas and our fun evening chats.
Follow us on Twitter @SuperluminalSft.